Temporal Similarity Search (TSS)

This page introduces you to the similarity algorithms used in KDB-X and explains how to use Temporal Similarity Search (TSS) and Dynamic Time Warping (DTW) to perform a similarity search.

Many applications such as stock prices, IoT sensor readings, server performance metrics, audio signals, and more involve time series data. When working with such data, a common task is to find series that are similar to one another. Unlike static vectors, time series have an order and rhythm, which means traditional similarity measures don't always apply.

Temporal similarity algorithms address this challenge by comparing sequences across time. Two important methods in this area are Temporal Similarity Search (TSS) and Dynamic Time Warping (DTW). Both allow you to query time series data efficiently and find matches that are close in shape, even when there are differences in scale, offset, or timing.

Learn more about:

Note

Temporal Similarity Search is also known as Time Series Search. Both terms are used interchangeably and are equally correct.

TSS provides efficient subsequence matching within time series data. It locates segments in a dataset that resemble a query sequence, supporting fast comparisons even across very large collections. This makes it especially useful for pattern discovery, such as identifying where a particular temporal shape occurs in a dataset.

Z-normalization option

Z-normalization (sometimes called z-score normalization) is a statistical technique that rescales a sequence so that it has:

  • Mean = 0
  • Standard deviation = 1

For a time series, each value is transformed using the formula:

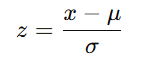
z-normalization formula

where:

  • x is the original data point
  • μ is the mean of the series
  • σ is the standard deviation of the series

This transformation removes differences in scale (how large the values are) and offset (baseline levels), leaving only the shape of the series for comparison.

For example, imagine two temperature readings:

  • Series A: [20, 22, 24, 26, 28]
  • Series B: [70, 72, 74, 76, 78]

Numerically they are quite different (°C vs °F), but their shapes are identical. After z-normalization, both will look the same: a sequence steadily increasing in equal steps.

Why it matters in TSS

By default, TSS applies z-normalization to both the query and candidate subsequences. This adjustment removes differences in scale and offset, allowing the algorithm to focus on the shape of the sequence. For example, two upward trends with different baselines appear similar to the algorithm.

If z-normalization is disabled, TSS instead compares the raw values directly. In this mode, both shape and magnitude affect similarity, making it suitable for use cases such as anomaly detection in sensor data or financial tick matching, where absolute values are critical.

Rule of thumb: enable z-normalization when pattern similarity is more important than scale, and disable it when absolute values matter.

Dynamic Time Warping (DTW)

DTW is a method for measuring similarity between time series that may be misaligned in time. Originally developed for speech recognition, DTW has become a standard tool in fields as diverse as finance, bioinformatics, and IoT analytics. Unlike simpler distance measures, DTW allows sequences to be "warped" along the time axis so that similar shapes can be matched even if one sequence is stretched, compressed, or shifted in time.

How it works

DTW calculates a similarity score by aligning two sequences in a way that minimizes the total distance between their points. Instead of comparing index-to-index (point 1 to point 1, point 2 to point 2, etc.), DTW builds a grid and finds an optimal path through this grid that pairs elements across sequences.

If one sequence runs "faster" than the other, DTW can align multiple points from one sequence to a single point in the other. DTW computes this alignment using dynamic programming, ensuring it finds the best global match rather than a local one. The output is both a similarity score and an alignment path that shows how the sequences map onto each other.

For example, two heart rate signals with the same pattern but different pacing will still align under DTW, where Euclidean distance would see them as very different.

When to use

DTW is useful when patterns matter more than precise timing.

  • Speech and audio analysis: matching spoken words regardless of speaking speed.
  • Finance: comparing price movements that occur at different rates across assets.
  • Medical and IoT sensors: detecting recurring physiological signals (for example, ECG, activity monitoring) even if cycles speed up or slow down.
  • User behavior analytics: aligning sequences of user events that happen at different speeds.

DTW benefits

  • DTW is flexible to handle shifts, stretches, or compressions in time.
  • It captures similarity in shape rather than absolute time alignment.
  • Applicable across many domains with sequential data.

Comparing TSS and DTW

Both TSS and DTW are designed to measure similarity between time series, but they emphasize different aspects:

  • TSS with z-normalization enabled focuses on shape-based comparisons, ignoring scale and offset differences.
  • TSS with z-normalization disabled works on raw values, making it sensitive to magnitude as well as shape.
  • DTW allows flexible alignment in time, so similar patterns can match even if they occur at different speeds or with local shifts in timing.

In short, use TSS for fast subsequence matching but use DTW for patterns that may be stretched or compressed in time.

Next steps